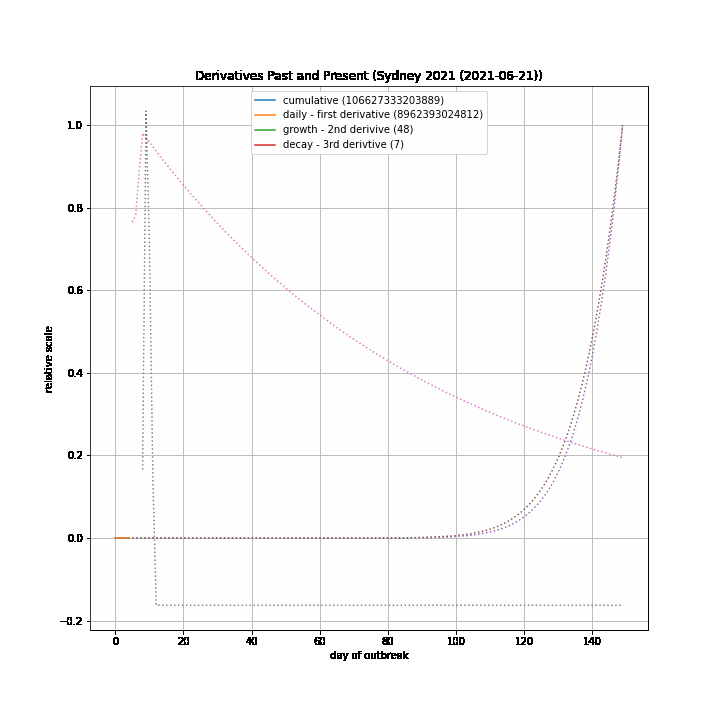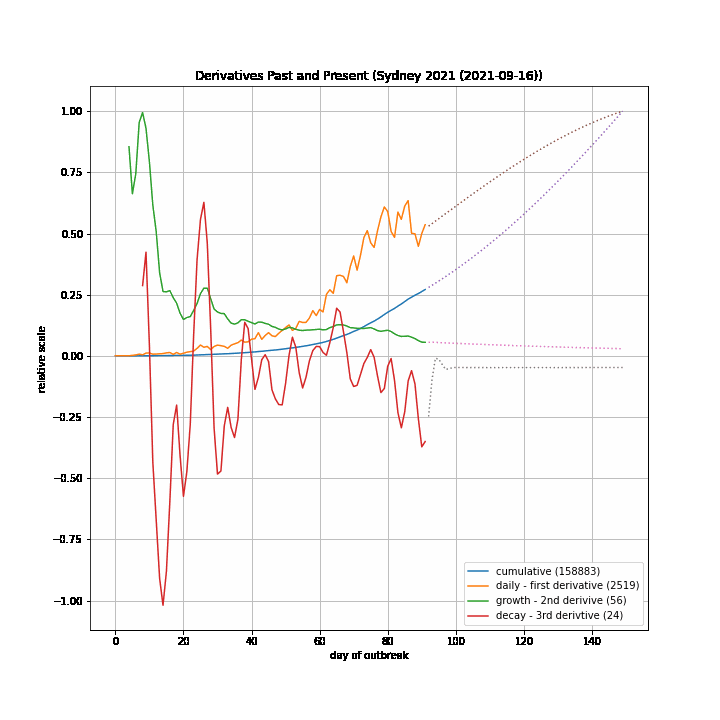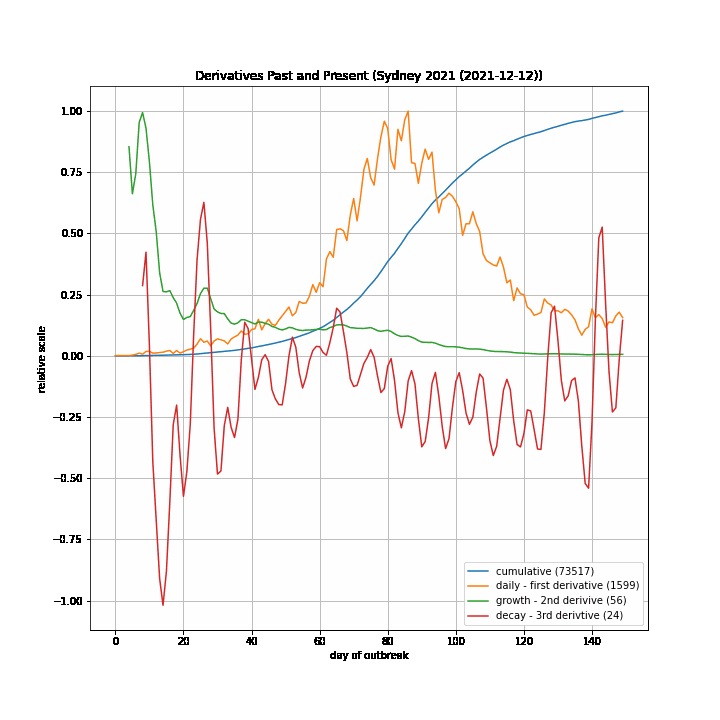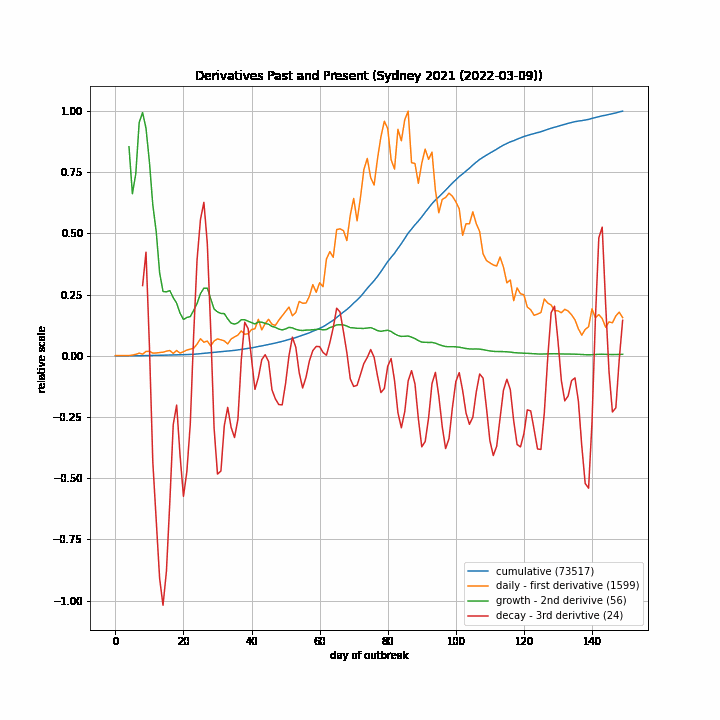
Growth Model¶
If the model was perfect, tbe following would be true:
$
\space\space\space\space\space\text{cumulative}_{t+1} = (1+\frac{\text{g}_t}{100})\times\text{cumulative}_t
$
In practice, the growth rate, $g_t$, is estimated by fitting a linear regession through a set of points:
$
\space\space\space\space\space(t-k, \ln{(\text{cumulative}_{t-k})})
$
for k = 0..4. This yields parameters of a linear reqregssion:
$
\space\space\space\space\space\ln(\text{cumulative}_t) = m \times t + b
$
Raisng e to each side, yields:
$
\space\space\space\space\space\text{cumulative}_t = (e^m)^t \times e^b = e^m \times (e^m)^{t-1} \times e^b = e^m \times \text{cumulative}_{t-1}
$
The growth rate, $g_t$, is thus:
$
\space\space\space\space\space g_t = (e^m-1) * 100
$
The minimum growth rate $g_{t,min}$ is defined as:
$
\space\space\space\space\space g_{t,min} = min(\{k: 0 \le k < 5: g_{t-k}\})
$
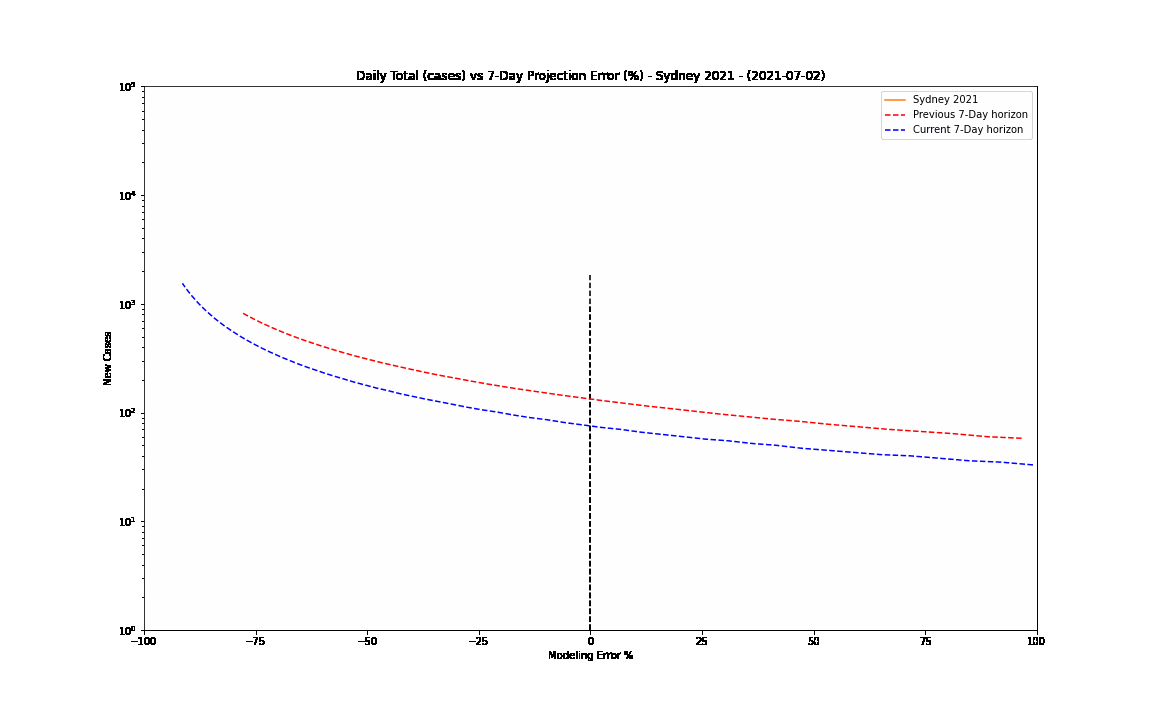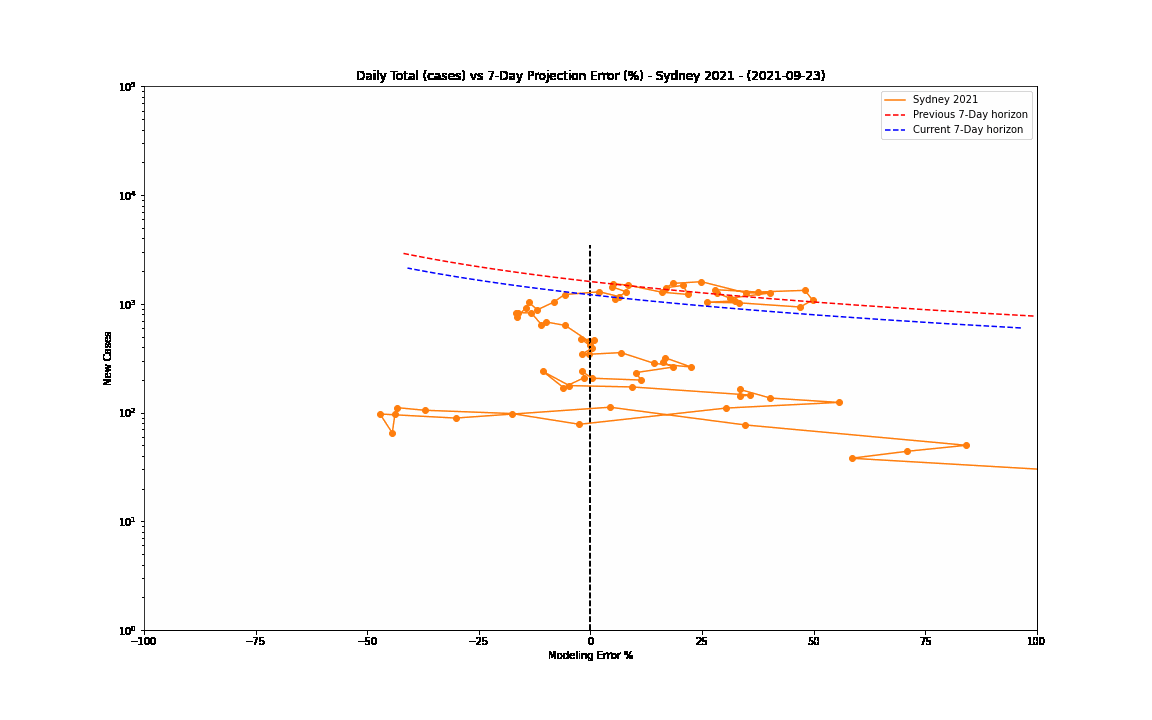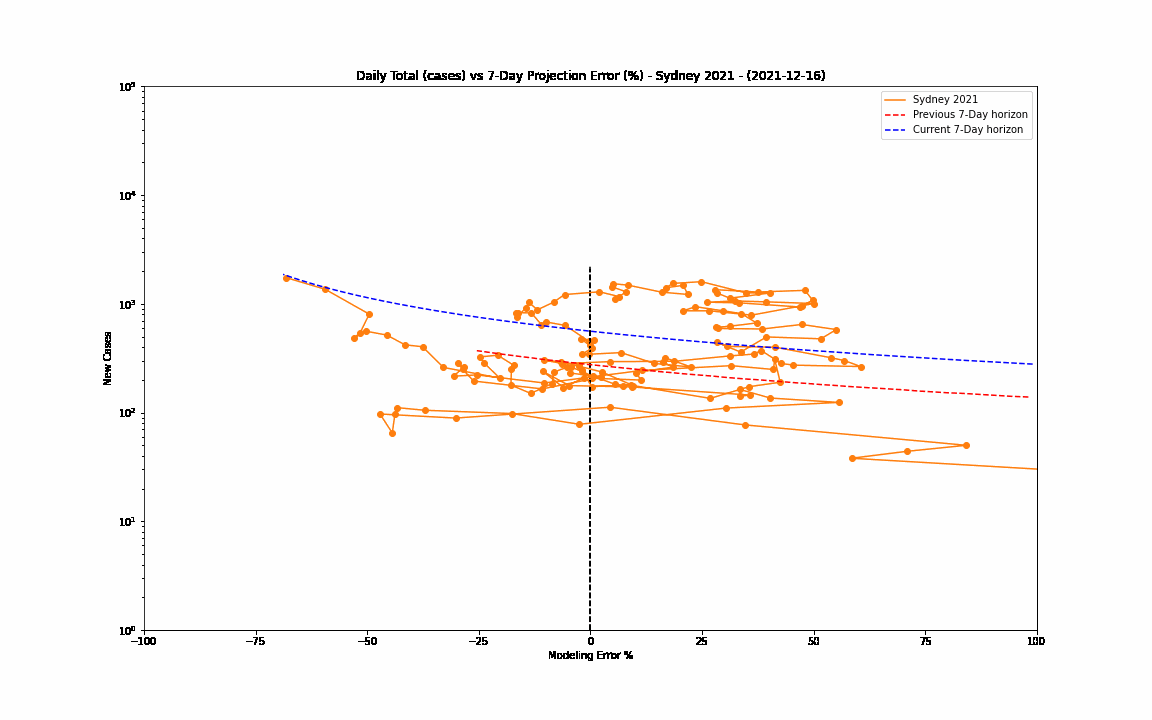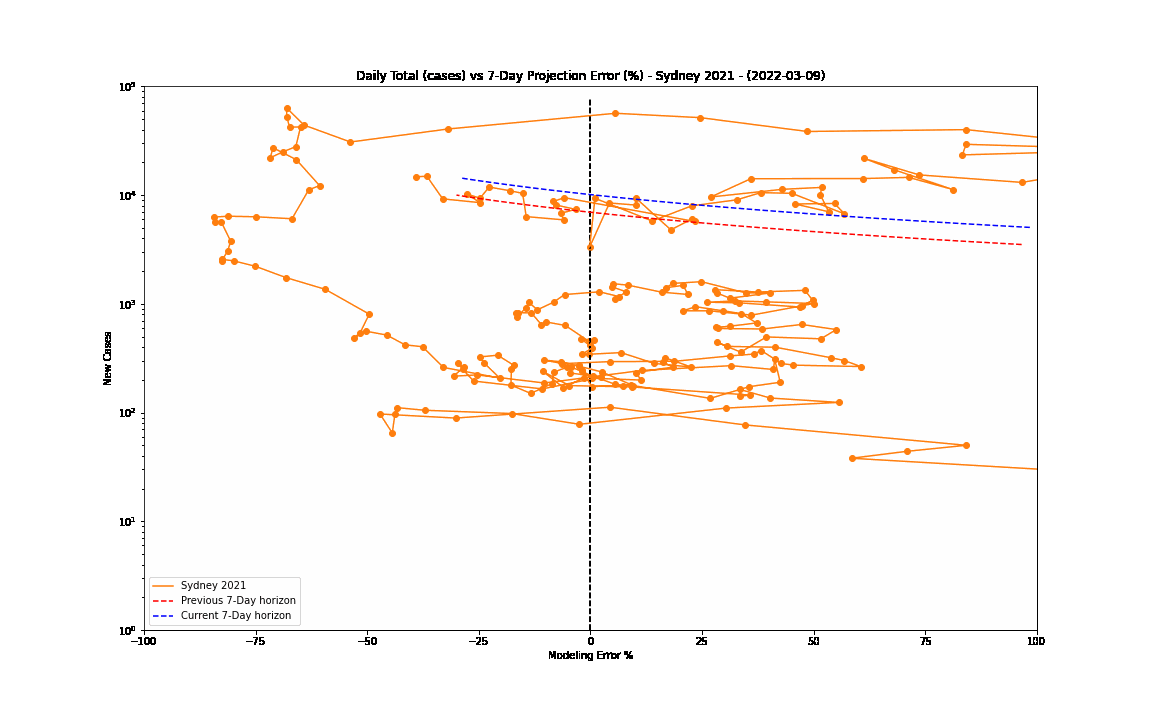
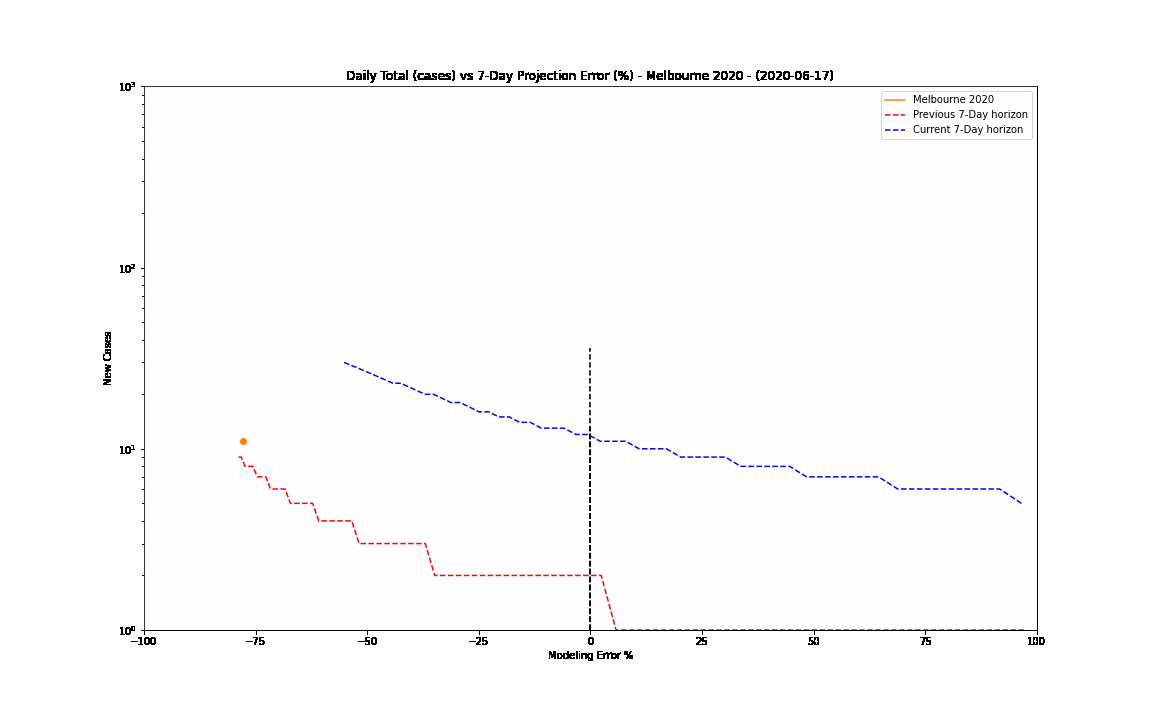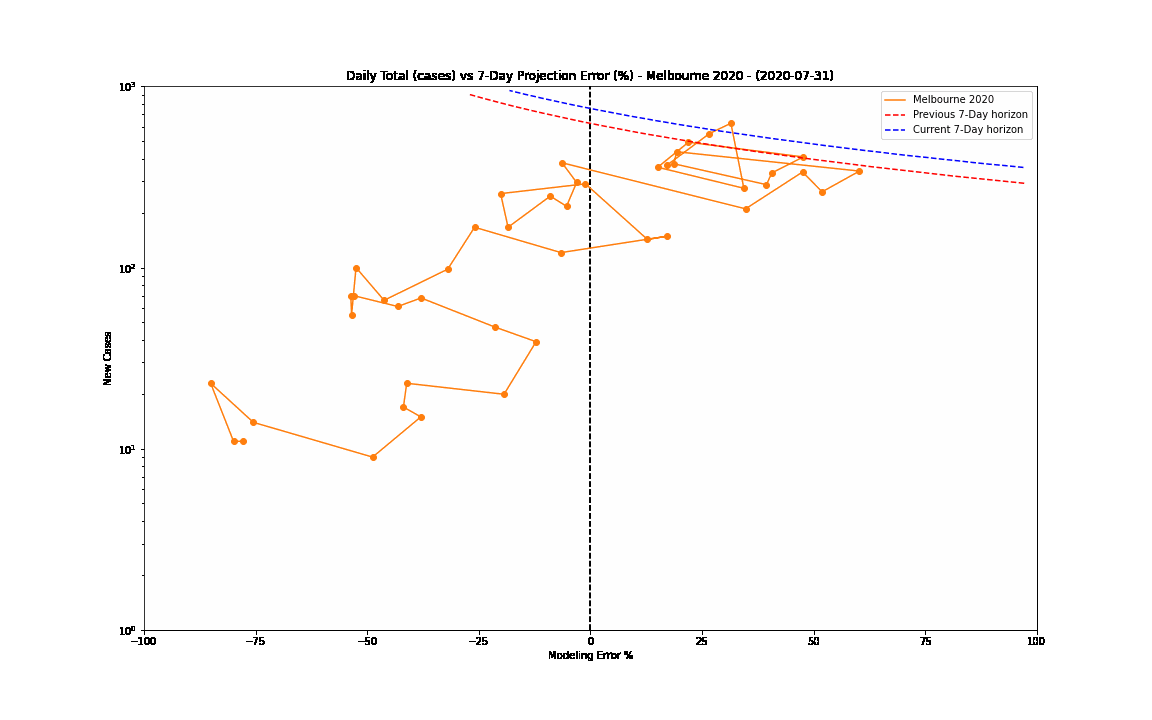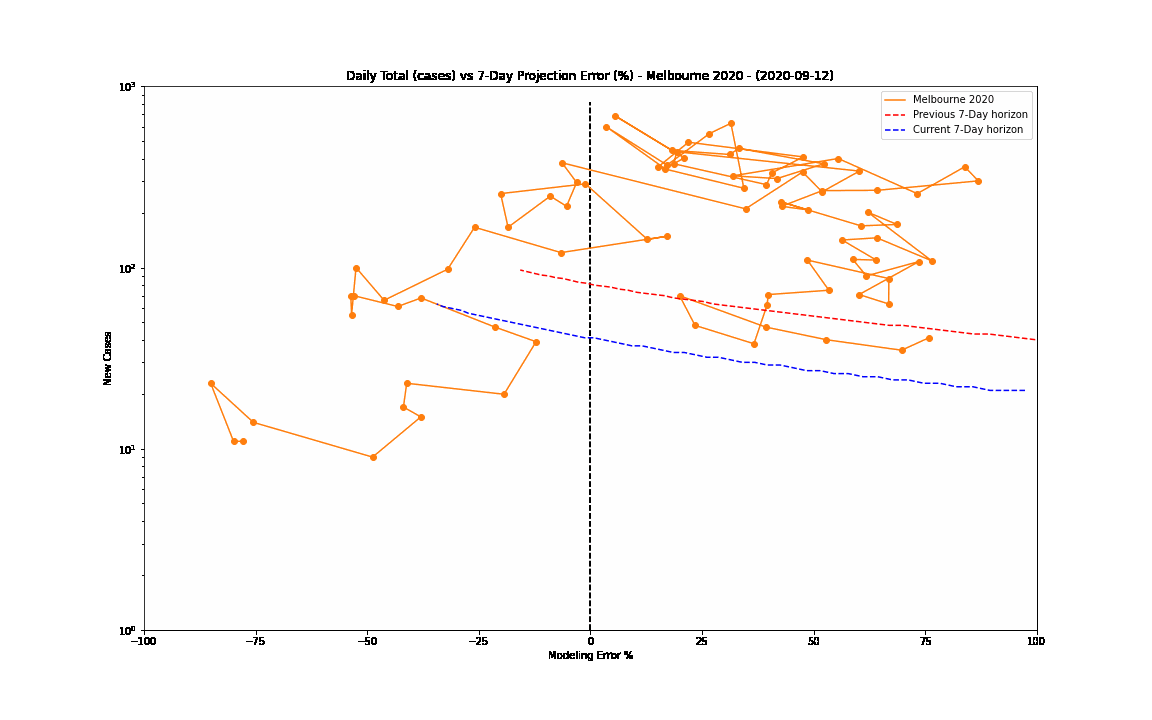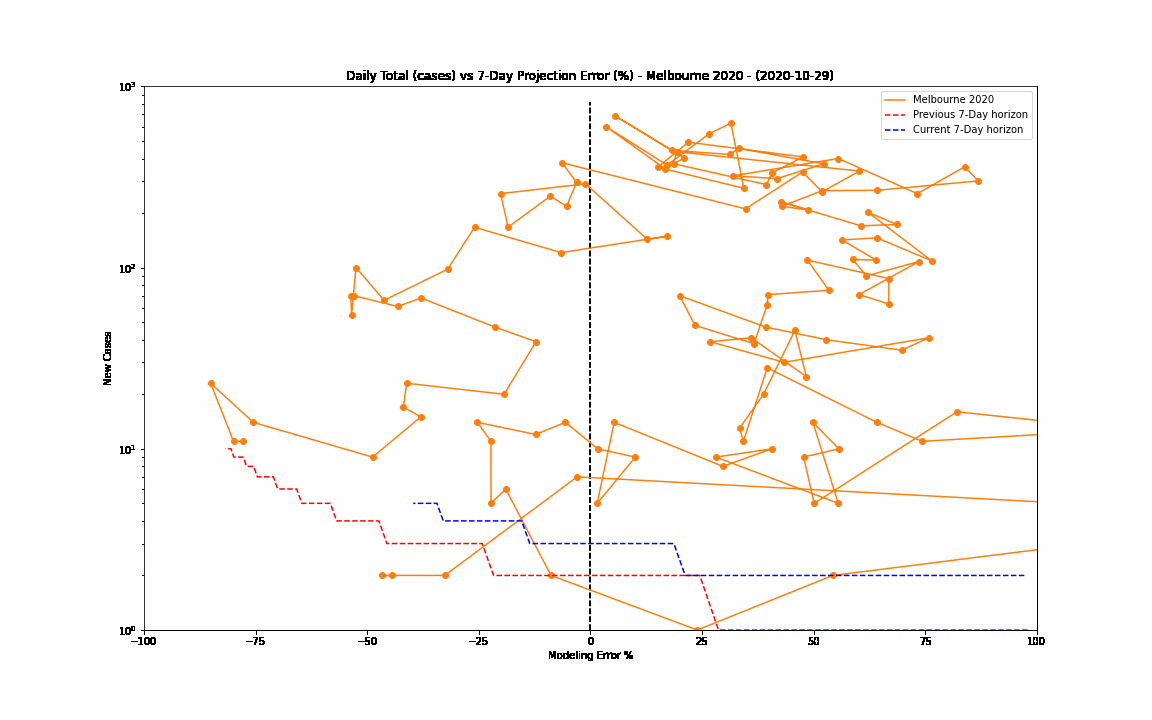
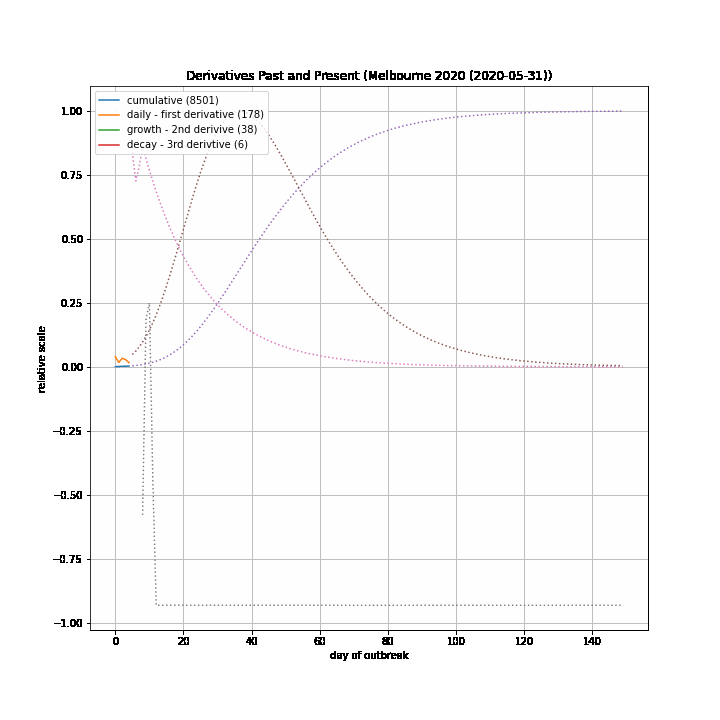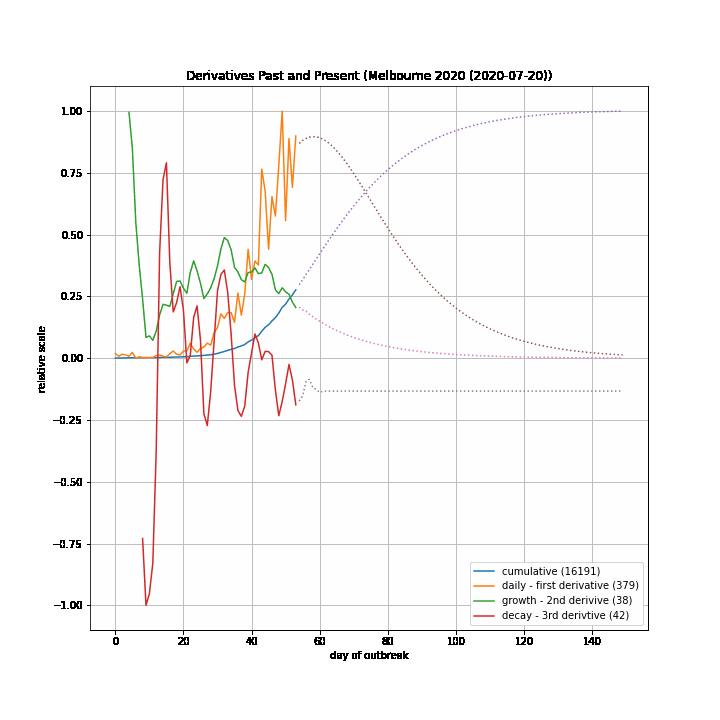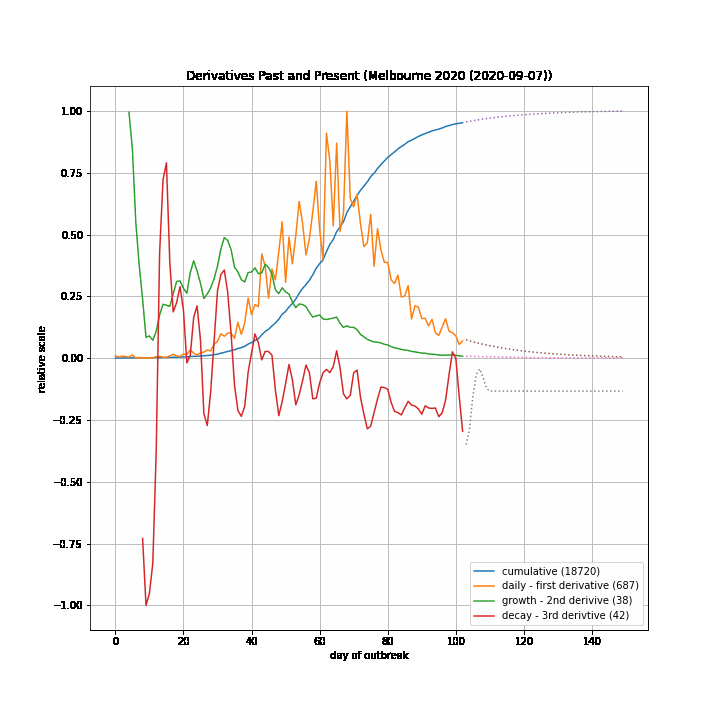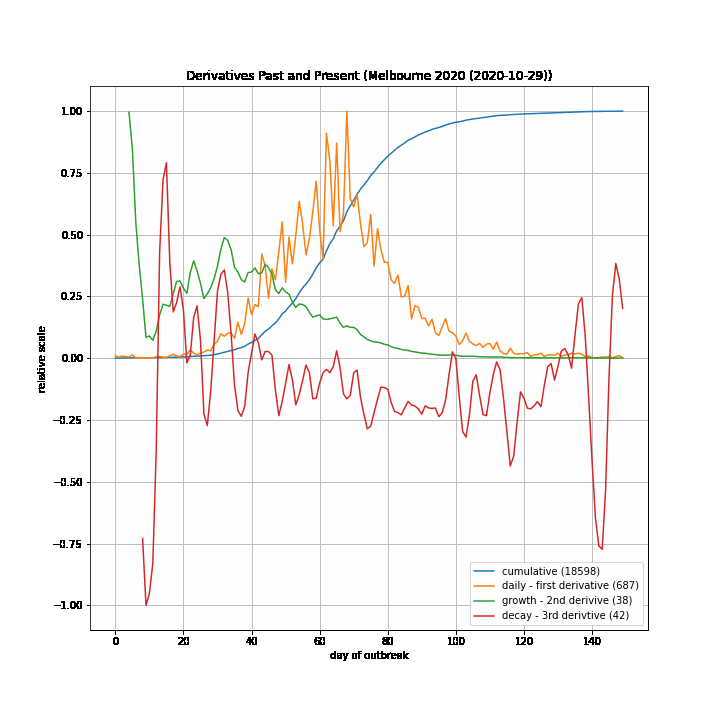
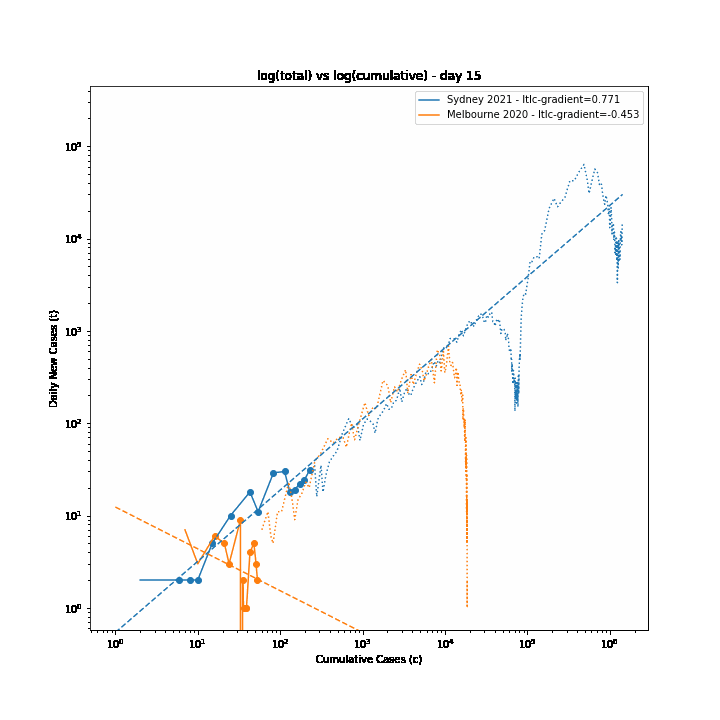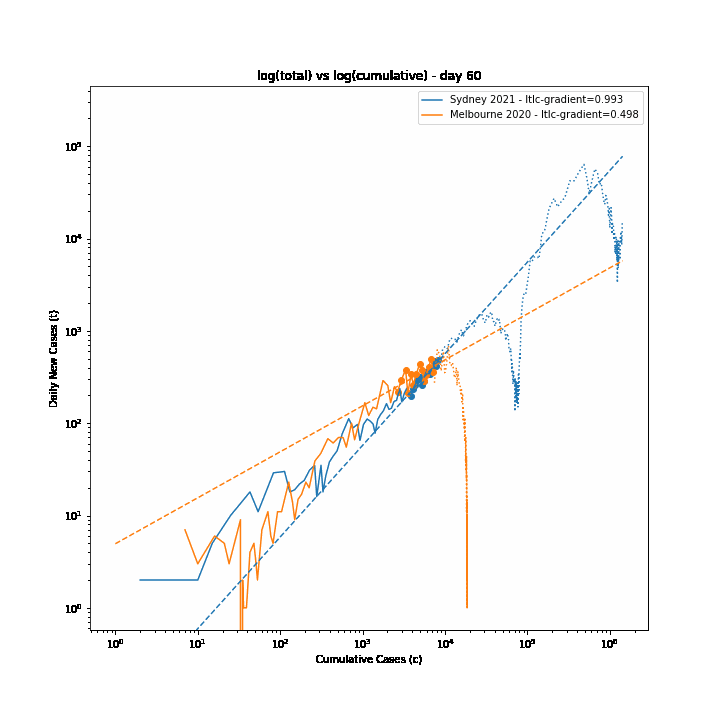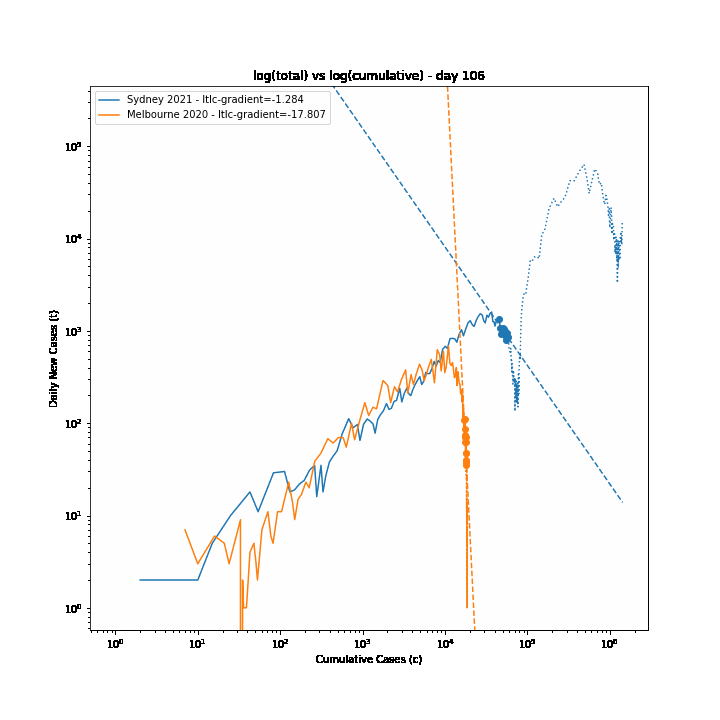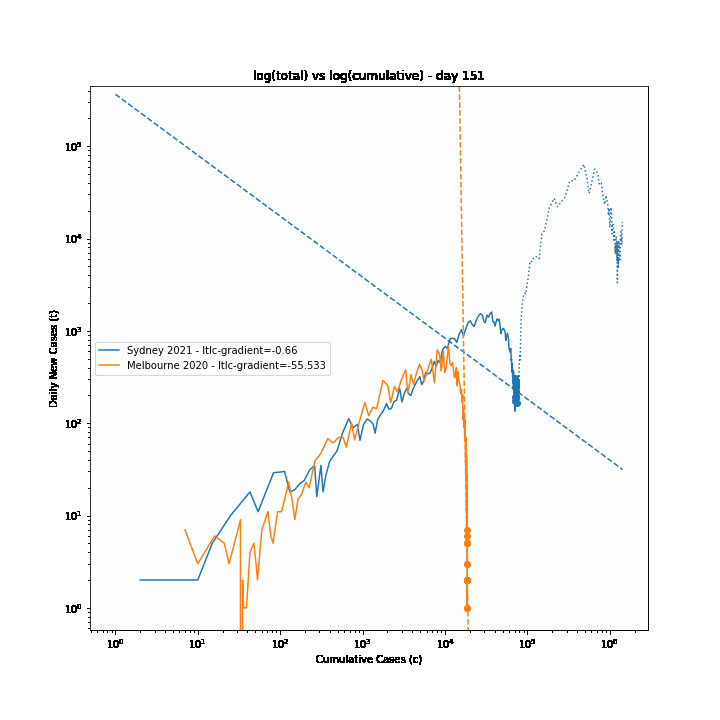
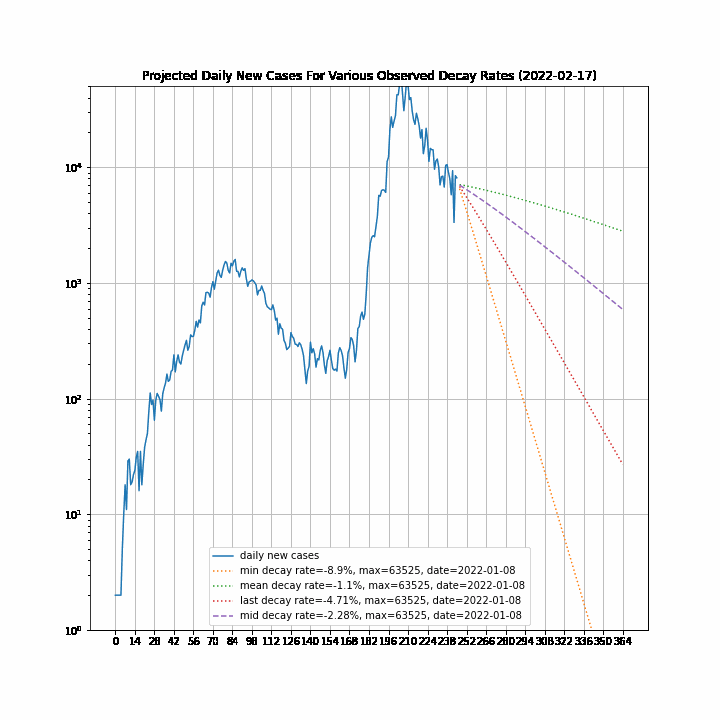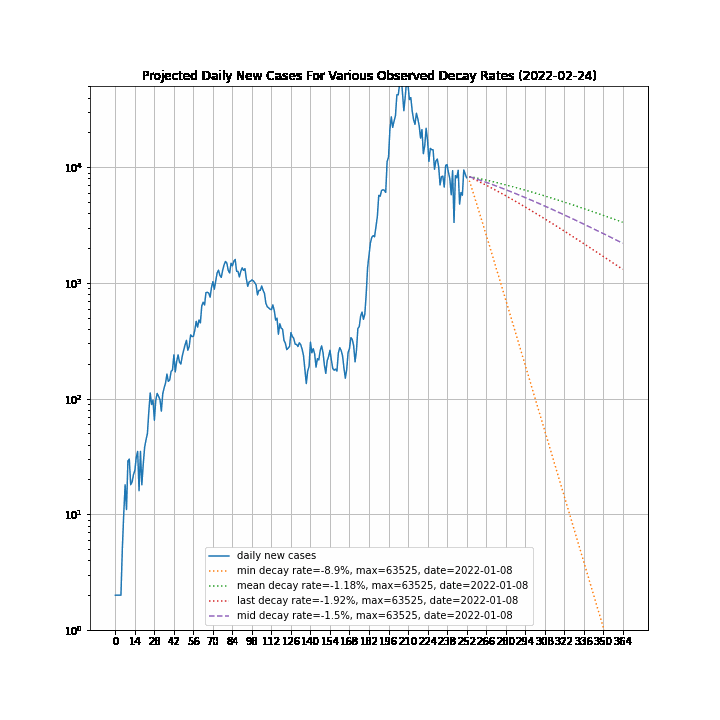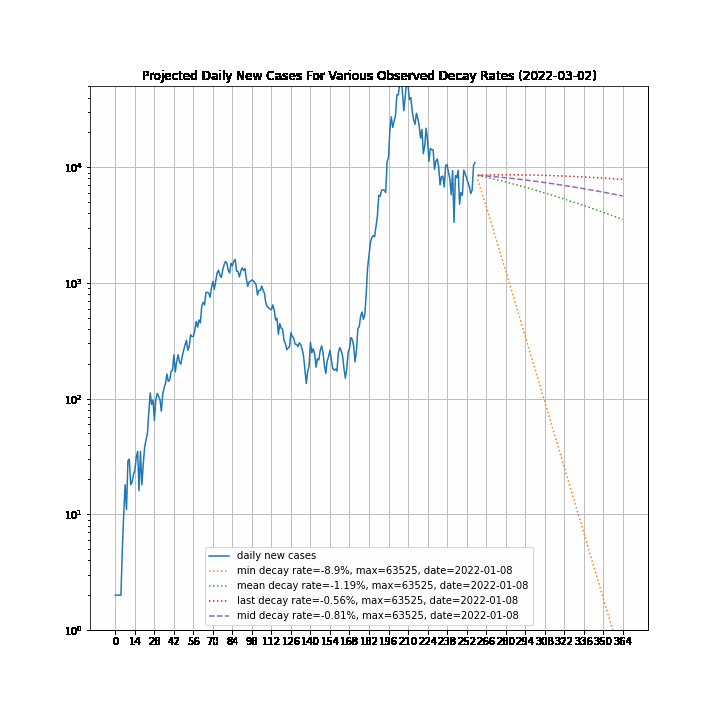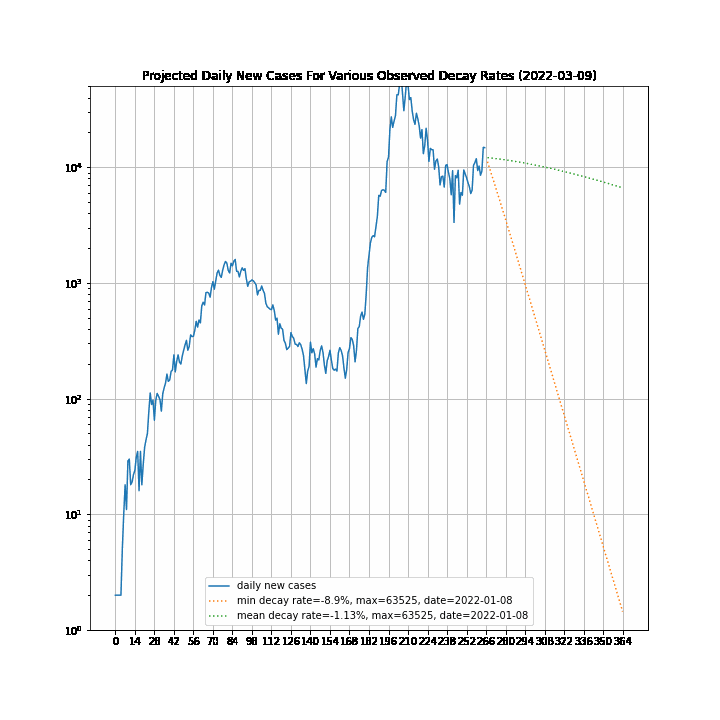
The 7-day forward projection of the cumulative total, $projection_t$ used on the so-called "hedgehog plot" uses $g_{t,min}$ since this was observed to provide closest fit to the Melbourne 2020 outbreak, particularly in the later stages.
$
\space\space\space\space\space \text{projection}_t = (1+\frac{g_{t-7,min}}{100})^7 \times \text{cumulative}_{t-7}
$
The intuitive justification is that because the growth rate eventually starts to decay, a fit to the last 5 days growth is going to tend overestimate the growth in the next 5 days so choosing the minimum observed growth rate estimate is more likely to be closer to true growth rate rather than the very latest estimate.
The replication factor, $R_{eff}$ is defined as:
$
\space\space\space\space\space R_{eff} = (1+\frac{g_t}{100})^5
$
The doubling period, in days, is defined as:
$
\space\space\space\space\space \text{doubling period}_t = \ln{(2)}/\ln{(1+\frac{g_t}{100})}
$
The table below documents various calculated parameters.
- date - the reporting date
- cumulative - the cumulative cases to the reporting date. This is usually the day after the cases were "notified".
- total - the number of cases reported on the reporting date
- ols-growth-rate - $g_t$, growth rate obtained from exponential fit to previous 5-days cumulative amounts expressed as a percentage change of cumulative cases per day
- ols-growth-rate-min - $g_{t,min}$, minimum ols-growth-rate statistic calculated in previous 5 days
- ols-growth-rate-decay - an expoenential fit to the ols-growth-rate statistic in the previous 5 days expressed as a percentage change of the ols-growth-date per day
- doubling-period - doubling period (in days) implied by ols-growth-rate
- Reff - implied $R{eff}$, assuming a 5 day generation period